3 気体と三相(3):肺と酸素ボンベの基礎
気体の体積とモル数のお約束のおはなしです。
1モルの粒が気体になったとき、
標準状態なら、その体積は22.4ℓになります。
標準状態というのは、0℃で1気圧のこと。
粒は何でも構いません。
窒素でも、酸素でも、二酸化炭素でも。
1モル(6.02×10²³個の粒)の気体は、22.4ℓになります。
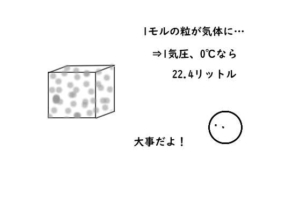
体積(ℓ)というのは、重さ(g)とは違った立体的な大きさのイメージ。
「1ℓペットボトル容器がどれくらい必要か」と考えれば、
ちょうどいい感じです。
気体は、ポンプなどの道具を使えば「押し込む」ことができます。
容器さえ頑丈なら
「1ℓの容器に2ℓ分の気体を押し込む」こともできます。
「押し込む」というのは、
「気体に圧力をかける」ということ。
この押し込む力と気体の体積には、一定の関係があります。
Aという力(PA)をかけたときの気体の体積(VA)と、
Bという力(PB)をかけたときの気体の体積(VB)には、
PA×VA=PB×VBという関係があります。
「同じ温度、同じモル数なら、
力と体積をかけたものは等しくなる」…ですね。
記号だとちょっとイメージしにくいので、具体例。
2ℓ分の空気があったとします。
1気圧のもとでは、2ℓ(1ℓペットボトル2個分)ですね。
2気圧をかけると…1ℓ(1ℓペットボトル1個分)になってしまいます。
先程の式に入れると
「1(1気圧:PA)×2(2ℓ:VA)=2(2気圧:PB)×1(1ℓ:VB)」です。
同じ気温とモル数なら、
かかる力と体積を掛け合わせたものは等しくなるのですね。
この関係は温度が変わっても使えます。
ただ、入れる温度には注意。
普段使う摂氏(℃)ではなく、
絶対温度(T=273+日常温度(℃))を入れますよ。
新しくできた式は
「(PA×VA)÷TA=(PB×VB)÷TB」です。
「絶対温度(T)を分母にする」ことが追加されましたね。
この式から分かってほしいことは、
「気体の圧力(P)は、容器の大きさ(V)と絶対温度(T)に左右される」です。
ここまで分かったら、空気の話を思い出してください。
空気は、窒素や酸素や二酸化炭素が混ざった気体でした。
それぞれの気体はどれくらいあるのかな…がこのおはなしの始まりでしたね。
どれくらい(モル数)は、気体の圧力(P)に比例します。
空気の圧力は、地上では1気圧。
窒素が約4/5で、酸素が約1/5、残り僅かに二酸化炭素…でしたね。
窒素の圧力をP(N₂)、酸素の圧力をP(O₂)、
二酸化炭素の圧力をP(CO₂)とすると、
1気圧≒P(N₂)+P(O₂)+P(CO₂)です。
「約(≒)」なのは、他にも混ざっている気体があるから。
大まかにはP(N₂)が0.8気圧、P(O₂)が0.2気圧。
P(CO₂)はごくわずか…です。
このときの気体の圧力を「分圧」と呼んでいます。
酸素分圧と言われたら、
「酸素の粒による圧力」のことですね。
…もうそろそろ「こんなこと勉強して何になるのさぁ!」と
言いたくなるころですね。
次回は「肺の交換システムと血圧」のおはなしに入りますよ。